最小二乘与最大似然参数估计及Python实现

共计 2020 个字符，预计需要花费 6 分钟才能阅读完成。

最小二乘法曲线拟合参数估计：
简单起见，这里以一元线性回归为例进行介绍：
假设我们获取了一组样本点数据：
利用最小二乘法用多项式曲线拟合这组样本点:
1、设拟合多项式为：
2、样本点到该曲线的距离平方和为：
目标函数为：
上式对参数求偏导有：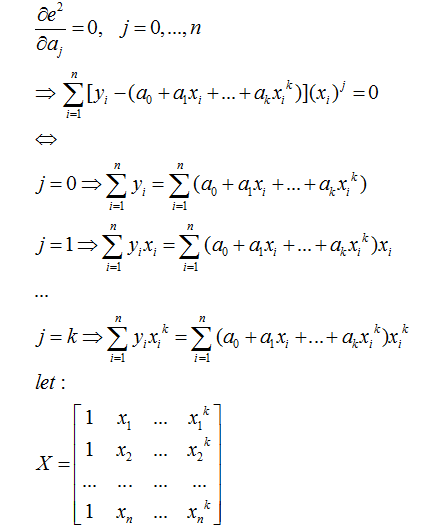
则上式等价于：
若X’X的逆矩阵存在：
是一个解析解(即一步到位的解法)
在测试中，我们假设训练样本是在曲线y=(x2-1)3+(x-0.5)2+3sin(2x)的基础上对x和y做随机拉伸处理生成的，我们假设拟合多项式阶数为9（可以用交叉验证来获取），用上述方法拟合得到的结果如下图所示：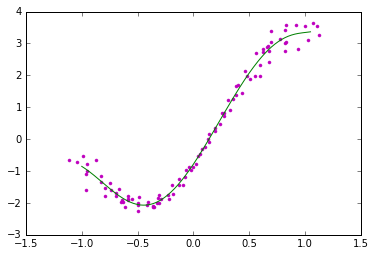
Python代码如下：

import numpy as np
import random
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111)

#阶数为9
order = 9

#生成样本点
x = np.arange(-1,1,0.02)
y = [((a*a-1)**3 + (a-0.5)**2 + 3*np.sin(2*a)) for a in x]
#ax.plot(x,y,color='r',linestyle='-',marker='')

x_a = [b1*(random.randint(90,120))/100 for b1 in x]
y_a = [b2*(random.randint(90,120))/100 for b2 in y]
ax.plot(x_a,y_a,color='m',linestyle='',marker='.')


#曲线拟合
#创建矩阵
#初始化而为数组
array_x =[[0 for i in range(order+1)] for i in range(len(x_a))]
#对二维数组赋值
for i in range(0,order+1):
    for j in range(0,len(x_a)):
        array_x[j][i] = x_a[j]**i
#将赋值后的二维数组转化为矩阵
matx=np.matrix(array_x)
matrix_A = matx.T*matx
yy = np.matrix(np.array(y_a))
matrix_B = matx.T*yy.T
matAA = np.linalg.solve(matrix_A,matrix_B).tolist()

#画出拟合后的曲线
xxa = np.arange(-1,1.06,0.01)
yya = []
for i in range(0,len(xxa)):
    yyy=0.0
    for j in range(0,order+1):
        dy = 1.0
        for k in range(0,j):
            dy*=xxa[i]
        dy*=matAA[j][0]
        yyy+=dy
    yya.append(yyy)
ax.plot(xxa,yya,color='g',linestyle='-',marker='')

ax.legend()
plt.show()

多元线性回归中参数的最大似然估计：
假设有m个训练样本(x, y)：
假定预测值与样本特征间的函数关系是线性的，即线性回归分析，就在于根据样本x和y的观察值，去估计函数h(x)，定义为：
1、对于第个训练样本，假设待估计函数h(x)与真实值y存在误差如下式所示：
假设：误差（即噪声）服从标准正太分布，则有：
2、单个样本下的组样本观测值的概率密度函数为：
3、根据最大似然概率的准则可得似然函数如下：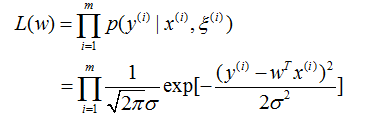
目标函数为：max(L(w))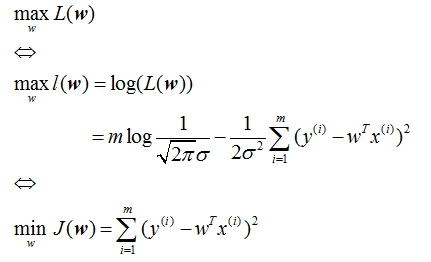
4、同第一部分，对上式求偏导数并令其等于0可得：
上式只在逆矩阵存在的时候适用。
在测试中，假设样本生成式为:y=0.5x+4*randuniform(0,1)*sin(2x)+3.5，用上述方法做多元线性回归得到的结果下图所示：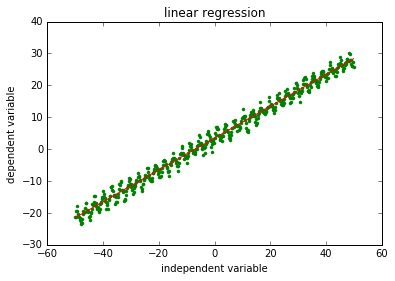
Python代码如下：

import numpy as np
import random
import matplotlib.pyplot as plt

#生成样本点
x = np.arange(-50,50,0.2)
array_x = []
array_y = []
for a in x:
    lineX = [1]
    lineX.append(a)
    array_x.append(lineX)
    array_y.append(0.5*a + 3.5 + random.uniform(0,1)*4*np.sin(2*a))

#线性回归
xMat = np.mat(array_x)
yMat = np.mat(array_y).T
xTx = xMat.T*xMat
w = xTx.I*xMat.T*yMat

y = xMat*w

#画图
plt.title("linear regression")
plt.xlabel("independent variable")
plt.ylabel("dependent variable")
plt.plot(x,array_y,color='g',linestyle='',marker='.')
plt.plot(x,y,color='r',linestyle='-',marker='')
plt.show()