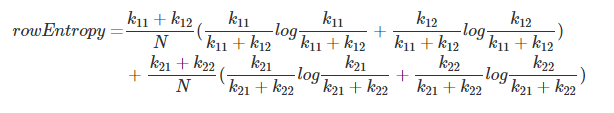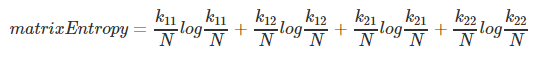共计 1598 个字符，预计需要花费 4 分钟才能阅读完成。
摘要：
在机器学习中常用到各种距离或者相似度，今天在看美团推荐系统重排序的文章时看到了loglikelihood ratio 相似度,特总结起来。以后有时间再把常用的相似度或者距离梳理到一篇文章。
背景：
记录loglikelihood ratio 相似度概念
总结：
下表表示了Event A和Event B之间的相互关系，其中：
k11 ：Event A和Event B共现的次数
k12 ：Event A发生，Event B未发生的次数
k21 ：Event B发生，Event A未发生的次数
k22 ：Event A和Event B都不发生的次数
则logLikelihoodRatio=2 * (matrixEntropy – rowEntropy – columnEntropy)
其中
rowEntropy = entropy(k11, k12) + entropy(k21, k22)
columnEntropy = entropy(k11, k21) + entropy(k12, k22)
matrixEntropy = entropy(k11, k12, k21, k22)
(entropy为几个元素组成的系统的香农熵)
下面举一个实际的例子：
我以一个实际的例子来介绍一下其中的计算过程：假设有商品全集I=｛a,b,c,d,e,f｝，其中A用户偏好商品{a,b,c}，B用户偏好商品{b,d}，那么有如下矩阵：
- k11表示用户A和用户B的共同偏好的商品数量，显然只有商品b，因此值为1
- k12表示用户A的特有偏好，即商品{a,c}，因此值为2
- k21表示用户B的特有偏好，即商品d，因此值为1
- k22表示用户A、B的共同非偏好，有商品{e,f}，值为2
此外我们还定义以下变量N=k11+k12+k21+k22，即总商品数量。
计算步骤如下：
- 计算行熵
注：代码中k11+k12与k21+k22均被约掉了，分母N也省去了
- 计算列熵
- 计算矩阵熵
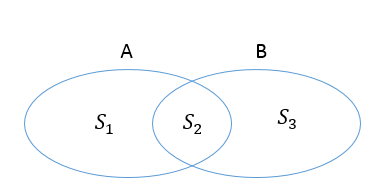
如何来解释这个相似度的计算方式呢？我们先来看看行熵、列熵和矩阵熵分别代表什么含义：行熵以用户A的偏好和非偏好来划分商品空间，很明显它是一个条件熵，我个人认为相对合理的解释是对于一个商品，在给定它是否属于A偏好的条件下，预测商品属于k11、k12、k21、k22四个空间中哪一个空间的不确定度；同理，列熵则代表给定商品是否属于B偏好的条件下，预测商品属于k11、k12、k21、k22四个空间中哪一个空间的不确定度；矩阵熵则表示在没有任何条件下，预测商品属于四个空间中哪一个空间的不确定度。我们以下图来看：
在给定A偏好与否的条件，预测商品属于哪一个空间的不确定度为S1+S2；在给定B偏好与否的条件下，不确定度为S2+S3；在不给定任何条件下，预测商品属于哪一个空间的不确定度为S1+S2+S3。我的理解这个S2S2表示的就是给定A、B偏好条件下的公共的不确定度，其表达的就是如果A喜欢某个商品，对B也具有协同效应；如果B喜欢某个商品，对A也具有协同效应，这种公共不确定度或者说是关联其实反映的就是A用户与B用户的相似程度。由于前面计算熵的时候没有加上负号，步骤四中正好得到一个(−S2)，就变成正数了，至于为什么乘上2及1N1N去哪里了我也不清楚，但这只是一种幅度变换，不影响相对关系。
- 计算相似度
UserSimilarity=2∗(matrixEntropy−rowEntropy−columnEntropy)
- 实现代码：https://github.com/Tongzhenguo/Java-codes/blob/master/src/main/java/data/code/similarity/logLikelihoodRatio.java
参考链接：
http://www.csdn.net/article/2015-01-30/2823783
http://blog.csdn.net/u014374284/article/details/49823557
