共计 5133 个字符,预计需要花费 13 分钟才能阅读完成。
一、Numpy
1.1 轴、维度及秩
1.1.1 轴
numpy数组中的轴不太容易理解,但是却非常重要。官方定义为:轴即维度(In Numpy dimensions are called axes.)。
对于二维数组,0轴即代表数组的行,1轴代表数组的列,对二维数组:
>>>arr1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> arr1
array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])为了验证上述结论,我们通过代码对每个轴方向的数字进行求和计算,如下:
>>> arr1.sum(axis=0)
array([12, 15, 18])
>>> arr1.sum(axis=1)
array([ 6, 15, 24])对于三维数组,这个问题就有点复杂了。给定如下的三维数组:
>>> arr = np.array([[[0, 1, 2, 3], [4, 5, 6, 7]], [[8, 9, 10, 11], [12, 13, 14, 15]]])
>>> arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])由轴的定义可知,数组arr有3条轴,编号分别为0、1、2,要直接看出来这三条轴分别对应什么方向有点困难。最好的办法就是先将三维数组降维成一个二维数组,这样就可以获得原数组的0轴、1轴。怎么降呢?把最内层数组作为一个整体来看待,即有:
A = [0, 1, 2, 3]
B = [4, 5, 6, 7]
C = [ 8, 9, 10, 11]
D = [12, 13, 14, 15]
arr = [[A, B],
[C, D]]可以看出通过这种变换,我们就把原数组从形式上转化成了一个二维数组,但是一定要注意这里的A、B、C、D均为一维数组,对它们进行操作时,要按照向量而非标量的运算法则进行。降维后的轴方向如下图所示:
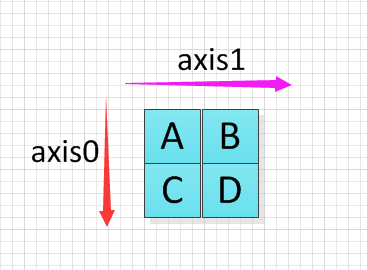
此时对0、1轴方向求和有:
# arr.sum(axis=0) = [A + C, B + D]
# A + C = [0+8, 1+9, 2+10, 3+11] = [8, 10, 12, 14]
# B + D = [4+12, 5+13, 6+14, 7+15] = [16, 18, 20, 22]
>>> arr.sum(axis=0)
array([[ 8, 10, 12, 14],
[16, 18, 20, 22]])
# arr.sum(axis=1) = [A + B, C + D]
>>> arr.sum(axis=1)
array([[ 4, 6, 8, 10],
[20, 22, 24, 26]])那么2轴方向呢?由于A、B、C、D均为一维数组,因此第三个周(轴2)即为最内层数组的行方向,如下图所示:
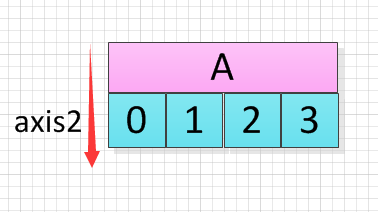
所以对轴2方向进行求和,实际上就是分别将A、B、C、D的元素求和(对一维向量应用sum函数,计算的是该向量所有元素之和),代码及结果如下:
# sum(A) = [0 + 1 + 2 + 3] = [6]
>>> arr.sum(axis=2)
array([[ 6, 22],
[38, 54]])由此可知,对于多维数组,numpy对轴的编号是先行后列,由外向内!实际中三维数组算是维度比较高的了,至于四维及以上的不太常见,因此没必要讲,但是为了验证我们刚才提到的这个结论,我们再举一个四维数组来证明。
我们先生成一个4*2*2*2数组,代码如下:
>>> arr2 = np.arange(0, 32)
>>> arr2
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31])
>>> arr2.reshape(4,2,2,2)
array([[[[ 0, 1],
[ 2, 3]],
[[ 4, 5],
[ 6, 7]]],
[[[ 8, 9],
[10, 11]],
[[12, 13],
[14, 15]]],
[[[16, 17],
[18, 19]],
[[20, 21],
[22, 23]]],
[[[24, 25],
[26, 27]],
[[28, 29],
[30, 31]]]])为了手算出结果,同样的,我们需要对原数组进行降维,降维方法是将内部的二维数组分别用字母表示,即有:
A = [[ 0, 1], [ 2, 3]]
B = [[ 4, 5], [ 6, 7]]
C = [[ 8, 9], [10, 11]]
D = [[12, 13], [14, 15]]
E = [[16, 17], [18, 19]]
F = [[20, 21], [22, 23]]
G = [[24, 25], [26, 27]]
H = [[28, 29], [30, 31]]
arr2 = [[A, B],
[C, D],
[E, F],
[G, H]]降维后可知,对0、1轴求和的结果为:
>>> arr2.sum(axis=1)
array([[[ 4, 6],
[ 8, 10]],
[[20, 22],
[24, 26]],
[[36, 38],
[40, 42]],
[[52, 54],
[56, 58]]])同理可求出1轴求和结果:
四维数组一共有4个轴,至此我们已经把最外层的两个轴(0、1)计算完了,还剩下4-2=2个轴,这两个轴(2,、3)按照我们上面的结论,分别对应内层数组的行(轴0)、列(轴1)。对轴2、3进行求和计算实际上就是对这些二维数组的行、列分别进行求和。
以A = [[0,1], [2, 3]]来说,对其0、1轴求和分别等于[2, 4]、[1, 5],同理可求出剩余的二维数组的相关值,因此对原四维数组轴2、3求和的结果为:
>>> arr2.sum(axis=2)
array([[[ 2, 4],
[10, 12]],
[[18, 20],
[26, 28]],
[[34, 36],
[42, 44]],
[[50, 52],
[58, 60]]])
>>> arr2.sum(axis=3)
array([[[ 1, 5],
[ 9, 13]],
[[17, 21],
[25, 29]],
[[33, 37],
[41, 45]],
[[49, 53],
[57, 61]]])这就证明了我们上面的结论是完全正确的,当维度 时,原理是一样的,只是稍微繁琐一些。需要注意的是,如果我们要手算,应该进行降维,降维后的维度最好是2,因为这是我们能直观理解的最佳维度,外层计算完后,计算内层时,内层元素进行维度还原时,也最好是二维数组。
1.1.2 维度
numpy数组中的维度(dimension)官方定义说是指轴的个数,通俗点将,就是你要取得这个数组里面的某个元素必须使用的索引的个数,比如有如下数组:
arr1 = np.array([[1,2], [7,5]])我们要使用arr1[1][0]来取得数组中的元素7,即用了两个索引来获得数组元素,因此数组arr1的维度即为2。
1.1.3 秩
官方定义中,秩即为轴的个数。
1.2 数组转置
1.2.1 转置概述
有了上面多维数组轴的概念,要理解数组的转置就容易多了。对于数组的转置,当维度N≤2时即表示二维数组的转置,其含义非常明确(行列互换),也很容易理解,但是当维度N≥3时,就不太直观了。书中P97-98关于三维数组的转置(transpose)和轴对换(swapaxes)的描述过于简单,也比较抽象,导致新手有点雾里看花的感觉,对这个问题我认真思考了三天,经过大量的手工推演及编码验证,才搞清楚了它的原理。因为五维及以上的转置,手工推演已经失去了价值和意义并且工作量浩大,所以这里我们仅对三维及四维数组转置做推导,更高维度的原理相同。
1.2.2 三维数组
生成一个三维数组(2*2*4),代码如下:
>>> import numpy as np
>>> arr = np.arange(0,16)
>>> arr
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
>>> arr = arr.reshape(2,2,4)
>>> arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])现在对其按任意轴序进行转置,假定轴序为(2, 0, 1),则转置代码为:
arr.transpose((2, 0, 1))transpose()函数接受的是一个由轴编号组成的有序元组,表示变换后的新数组的轴编号顺序。上述代码的含义就是:将原数组的轴2变换为新数组的轴0,原数组的轴0变换为新数组的轴1,原数组的轴0变换为新数组的轴1。
以上述数组来说,变换后的结果是怎样的呢?按照网上资料的做法,可以分别计算出每个元素变换后的索引,然后就可以得到变换后的数组,比如对元素6,变换前其索引为[0][1][2],变换后的索引则变成了[2][0][1],数组小的时候,这样做还可以,当数组非常大的时候,一个个去计算就非常不明智了,并且容易算错。我们需要一种更为高效、准确的方法——轴推导法。
轴推导法的思想主要有以下三步:
1. 定维度。根据变换前后各个轴轴向维度不变原理,可以确定变换后的数组形式;
2. 定内层。先确定最内层元素的形式;
3. 递归。确定内层元素后,由内向外,逐层确定元素形式及内容。
具体推导过程为:
1. 定维度。变换前各个轴的维度(注意:这里的维度是指各个轴方向元素的个数,与数组的维度有所区别。)如下:
| 轴号 | 0 | 1 | 2 |
|---|---|---|---|
| 维度 | 2 | 2 | 4 |
| 矩阵形式:2 * 2 * 4 |
则变换后矩阵的形式为:4(轴2) * 2(轴0) * 2(轴1),矩阵写出来的形式如下:
\[ \begin{align*} \huge \lbrack \ \LARGE &\lbrack \ \lbrack \ \square \ , \ \square \rbrack \ , \ \lbrack \ \square \ , \ \square \rbrack \ \rbrack , \\ &\lbrack \ \lbrack \ \square \ , \ \square \rbrack \ , \ \lbrack \ \square \ , \ \square \rbrack \ \rbrack , \\ &\lbrack \ \lbrack \ \square \ , \ \square \rbrack \ , \ \lbrack \ \square \ , \ \square \rbrack \ \rbrack , \\ &\lbrack \ \lbrack \ \square \ , \ \square \rbrack \ , \ \lbrack \ \square \ , \ \square \rbrack \ \rbrack \huge \ \rbrack \end{align*} \]
其中的代表原数组中的任意一个数字。
2. 定内层。对于内层数组而言,是一个1 × 2的矩阵,变换后的新数组的轴2(即最内层数组的行方向)是原来的数组的轴1(即最外层数组的列方向),原数组的列方向数字依次为0,1,2,3⟶,所以变换后最内层数组的行方向元素依次为:
3. 递归。内层数组首元素确定后,我们还需要根据外层数组的行列才能完全确定变换后的数组。上可知,变换后的数组的列方向是原数组的行方向,于是得到列首元素:
注意:这里首行的列元素顺序为0,4,8,12⟶而不是0,8,4,12⟶,因为0、4才是属于不同行同列的元素。
再根据变换后数组的行方向是原数组的列方向,可以分别得到4、8、12下面的元素,最后结果为:
代码运行结果与我们的推导完全一致,如下:
>>> arr.transpose(2,0,1)
array([[[ 0, 4],
[ 8, 12]],
[[ 1, 5],
[ 9, 13]],
[[ 2, 6],
[10, 14]],
[[ 3, 7],
[11, 15]]])1.2.3 四维数组
四维数组的变换与三维数组类似,只是需要先确定最内层数组的行、列方向,在变换中一定要注意的是:保持元素的对应关系(异行同列,异列同行)!如果不确定,可以使用元素索引来辅助分析。比如,对三维数组中索引为 的元素,按轴序(1,2,0)变换后,索引变为,也就是说原数组第一项的第一项中的元素变换后,是新数组的第一项的所有项的首元素。
1.3 轴对换
ndarray还提供了轴对换方法,名为swapaxes,它接受一对轴编号,然后将给定的两个轴的数据进行对换,它的作用于数组转置相同,只不过它每一次只能完成两个轴的交换,而transpose方法则可以是3个及以上,swapaxes用法如下:
>>> arr.swapaxes(1,2)
array([[[ 0, 4],
[ 1, 5],
[ 2, 6],
[ 3, 7]],
[[ 8, 12],
[ 9, 13],
[10, 14],
[11, 15]]])上述代码完成了原三维数组的轴2和轴1的交换。
转载自https://flat2010.github.io/2017/05/31/Numpy%E6%95%B0%E7%BB%84%E8%A7%A3%E6%83%91/




