ucb 一个简单的例子

2,485次阅读

没有评论

共计 2364 个字符，预计需要花费 6 分钟才能阅读完成。

这篇文章关于ucb 探索的简介和代码实现，大部分来自网上的一个大佬的文章，然后我试着改了写代码备注，新增了一个自己业务的示例。

让我们忘记探索阶段和利用阶段，仔细想想如何充分利用历史信息，找到最值得被推荐的菜：

观测 1: 如果一道菜已经推荐了k遍（获取了k次反馈），我们就可以算出菜做的好吃的概率：

$\overset{`} p=\frac{\sum rewards_{i}}{k}$

当k趋近正无穷时， $\overset{`} p$ 会趋近于真实的菜做的好吃的概率 p

观测 2: 现实当中一道菜被试吃的次数k不可能无穷大，因此估计出的好吃的概率 $\overset{`} p$ 和真实的好吃的概率 p 总会存在一个差值 $\Delta$

即 $$\overset{} p-\Delta \lt p \lt \overset{总是乐观地认为每道菜能够获得的回报是 $\overset{`} p+\Delta$ ，这便是著名的Upper **Confidence Bound (UCB) 算法，代码如下所示。

def UCB(t, N):
    upper_bound_probs = [avg_rewards[item] + calculate_delta(t, item) for item in range(N)]
    item = np.argmax(upper_bound_probs)
    reward = np.random.binomial(n=1, p=true_rewards[item])
    return item, reward

for t in range(1, T): # T个客人依次进入餐馆
   # 从N道菜中推荐一个，reward = 1 表示客人接受，reward = 0 表示客人拒绝并离开
   item, reward = UCB(t, N)
   total_reward += reward # 一共有多少客人接受了推荐

最后只需解决一个问题，真实的概率和估计的概率之间的差值 $\Delta$ 到底怎么计算呢？

在进入公式之前，让我们直观的理解影响 $\Delta$ 的因素：

对于被选中的菜，多获得一次反馈会使 $\Delta$ 变小，最终会小于其他没有被选中的菜
对于没被选中的菜， $\Delta$ 会随着轮数的增大而增大，最终会大于其他被选中的菜

下面我们正式介绍如何计算 $\Delta$ ，首先介绍Chernoff-Hoeffding Bound：

[Chernoff-Hoeffding Bound] 假设 reward1….rewardn是在[0, 1]之间取值的独立同分布随机变量，用 $\overset{`} p=\frac{\sum rewards_{i}}{k}$ 表示样本均值，用 p 表示分布的均值，那么有

$P{|\overset{`} p-p| \le \theta}\ge 1-2e^{-2n\theta^2}$

当 $\theta$ 取值为 $\sqrt{2lnT/n}$ 时 (其中T表示有T个客人，n表示菜被吃过的次数)，可以得到

$P{|\overset{`} p-p| \le \sqrt{2lnT/n} }\ge 1-\frac{2}{T^4}$

也就是说 $$\overset{} p-\sqrt{2lnT/n} \lt p \lt \overset{

当T=2时，成立的概率为0.875
当T=3时，成立的概率为0.975
当T=4时，成立的概率为0.992

可以看出 $\sqrt{2lnT/n}$ 是一个不错的选择。

最后，我们附上完整的代码，跟第一讲不一样的地方已经重点加粗标注。

import numpy as np

T = 1000 # T个客人
N = 10 # N道菜

true_rewards = np.random.uniform(low=0, high=1, size=N) # 每道菜好吃的概率
estimated_rewards = np.zeros(N) # 每道菜好吃的估计概率
chosen_count = np.zeros(N) #各个菜被选中的次数
total_reward = 0 

def calculate_delta(T, item):
    if chosen_count[item] == 0:
        return 1
    else:
        return np.sqrt(2 * np.log(T) / chosen_count[item])

def UCB(t, N):
    upper_bound_probs = [estimated_rewards[item] + calculate_delta(t, item) for item in range(N)]
    item = np.argmax(upper_bound_probs)
    # 生成奖励，这里为了验证算法使用的是 二项分布，如果是碰巧喜欢那么就是返回 1 否则 0 不喜欢
    # 对于推荐系统可以使用的点击或者不点击作为 reward 
    reward = np.random.binomial(n=1, p=true_rewards[item]) 
    return item, reward

for t in range(1, T): # T个客人依次进入餐馆
   # 从N道菜中推荐一个，reward = 1 表示客人接受，reward = 0 表示客人拒绝并离开
   item, reward = UCB(t, N)
   total_reward += reward # 一共有多少客人接受了推荐

   # 更新菜的平均成功概率
   estimated_rewards[item] = ((t - 1) * estimated_rewards[item] + reward) / t
   chosen_count[item] += 1

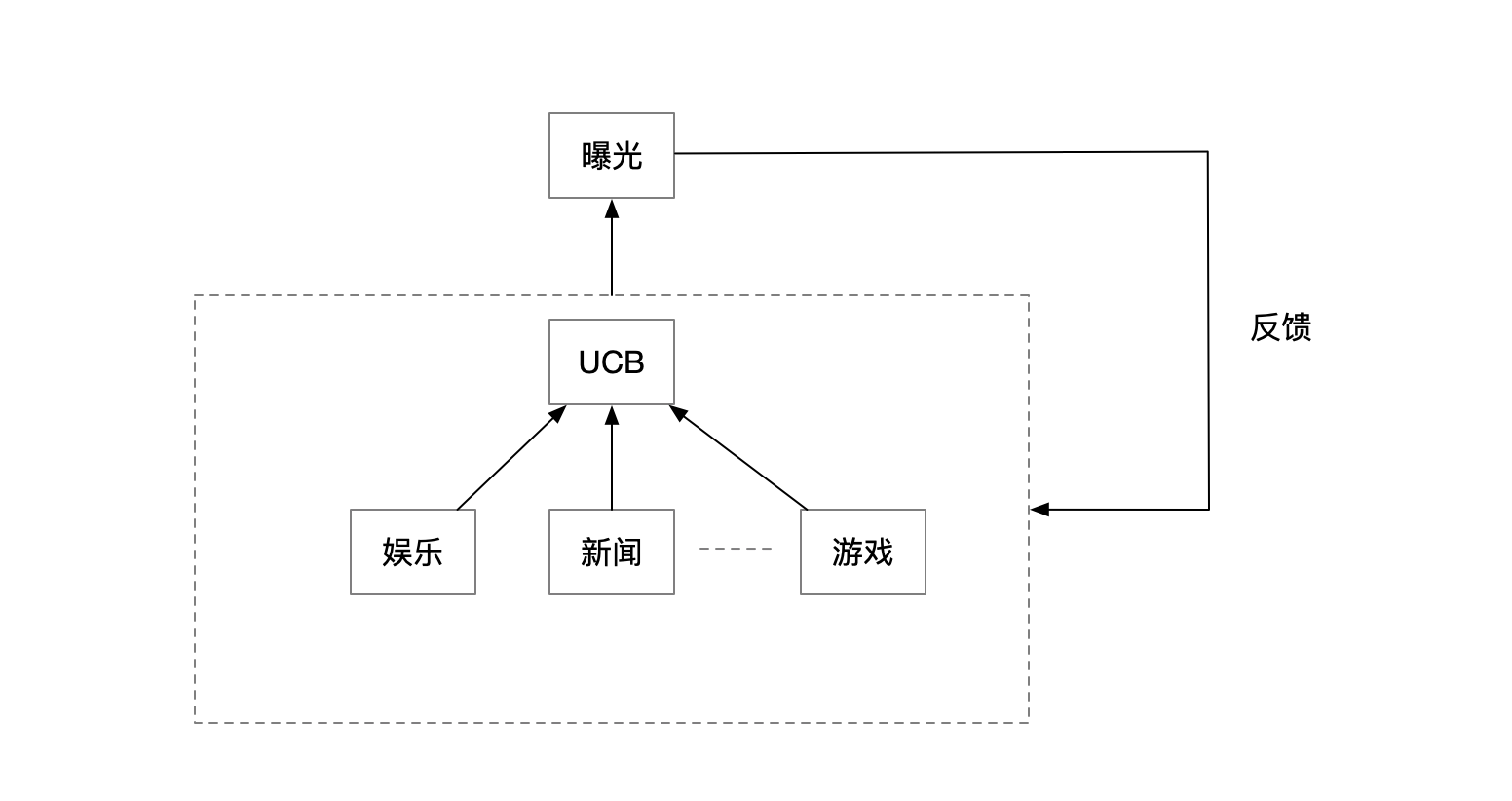
上面的描述是参考的一个大佬的文章，然后代码里有些备注我自己改了，然后我就自己现在做的视频探索画一个简单的示意图

ucb 一个简单的例子