共计 4545 个字符,预计需要花费 12 分钟才能阅读完成。
这种过拟合的处理称为正则化。 我们来学习一些最常用的正则化技术,并将其应用于实践中。
1.缩小神经网络的规模
防止过拟合最简单的方法是缩小模型的规模:模型中的可学习的参数数量(由层数和每层节点数决定)。 在深度学习中,模型中参数的数量通常被称为模型的能力。 直观地说,拥有更多参数的模型具有更强的记忆能力,甚至可以可以轻松地学习训练样本与其目标之间的类似字典的完美对应关系 –一种没有任何泛化能力的对应。但是这样的模型对于分类新的数字样本却没用,新的样本无法在这个“字典”找到它对应的类别。 一定要记住这一点:深度学习模型倾向于适应训练数据,但真正的挑战是泛化,而不是只对训练集样本适用就OK。
另一方面,如果网络的记忆资源有限(即参数较少),就不能轻易学习这种映射;因此,为了最小化损失,它必须要压缩信息 – 保留最有用的信息。因此,请记住,模型应该有足够的参数。不幸的是,没有一个公式可以用来确定神经网络正确的层数和层数所含的正确的节点数。我们必须评估一系列不同的网络架构(当然,在我们的验证集上,而不是我们的测试集上),以便为我们的数据找到合适的模型。找到合适的模型大小的一般过程是从相对较少的隐藏层和节点开始,逐渐增加隐藏层的节点数或添加新的层,直到看到验证集损失下降。
让我们在电影评论分类网络上试试这个。原来的网络是下面显示的:
from keras import models
from keras import layers
original_model = models.Sequential()
original_model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
original_model.add(layers.Dense(16, activation='relu'))
original_model.add(layers.Dense(1, activation='sigmoid'))
original_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['acc'])
让我们尝试用这个更小的网络:
model = models.Sequential()
model.add(layers.Dense(4, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
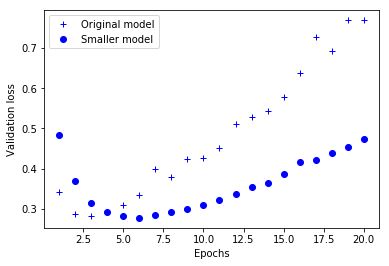
图1.1显示了原始网络和较小网络的验证损失的比较。点是较小网络的验证损失值,十字是原来较大的网络(记住,验证集损失越小表示模型越好)。
正如你所看到的,较小的网络在六个epoch而不是三个epoch之后才出现了过拟合。并且从过拟合开始,其性能变差得也更慢些。
现在,为了对比,让我们使用一个规模更大的网络 – 远远超过了问题的需求:
bigger_model = models.Sequential()
bigger_model.add(layers.Dense(512, activation='relu', input_shape=(10000,)))
bigger_model.add(layers.Dense(512, activation='relu'))
bigger_model.add(layers.Dense(1, activation='sigmoid'))
bigger_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])

图1.2显示了与原始网络相比更大的网络模型在验证集的表现。点是较大网络的验证集损失值,十字是原始网络。仅仅一个epoch后,更大的网络立即开始过拟合,其验证集损失值也是杂乱的。
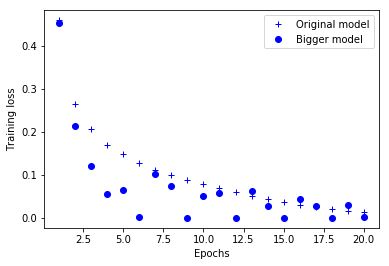
同时,图1.3显示了两个网络的训练集损失值随epoch的变化情况。正如你所看到的,更大的网络很快就会把训练集损失训练到接近零。 网络越大,训练数据学习的速度就越快(使训练损失很快降低),但是也更容易过拟合(导致训练和验证损失之间的巨大差异)。
2.权重正则化技术
你可能熟悉奥卡姆剃刀原则:给出两个解释,最可能正确的解释是更简单的一个 – 假设较少的解释。 这个原则也适用于神经网络的模型: 简单的模型比复杂的泛化能力好。
在这种情况下,一个简单的模型指的是模型:参数值的分布具有较小的熵(或者参数较少)。 因此,减少过拟合的一种常见方法是通过使权重只取小值来限制网络的复杂性,这使得权重值的分布更加规整。 这就是所谓的权重正则化,这是改变网络的损失函数来实现的,在原来的损失函数基础上增加限制权重的成本。这个成本有两种:
- L1正则化 – 所增加的成本与权重系数的绝对值成正比(权重的L1范数),权重稀疏化。
- L2正则化 – 所增加的成本与权重系数(权重的L2范数)的平方成正比。L2正则化在神经网络中也称为权重衰减。 不要让不同的名字混淆你:权重衰减在数学上与L2正则化相同。
在Keras中,通过将选择的权重正则化作为关键字参数传递给网络层来增加正则成本。 让我们在电影评论分类网络中添加L2权重正则化。
from keras import regularizers
model = models.Sequential()
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
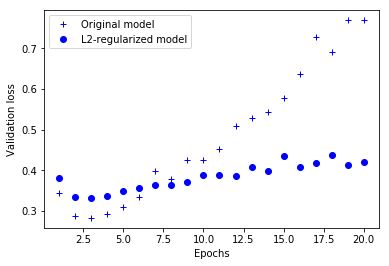
l2(0.001)意味着该层的权重矩阵中的每个系数将增加0.001 * weight_coefficient_value到网络的总损失。 请注意,由于这种惩罚只是在训练时间增加的,这个网络的损失在训练时比在测试时间要高得多。图2.1显示了L2正则化惩罚的影响。正如你所看到的那样,即使两个模型具有相同数量的参数,具有L2正则化的模型(点)也比参考模型(十字)更能减少过拟合。
除了L2正则化,你还可以使用以下Keras权重正则方法。
from keras import regularizers
regularizers.l1(0.001) # L1正则化
regularizers.l1_l2(l1=0.001, l2=0.001) # 同时进行L1和L2正则化
3.Dropout
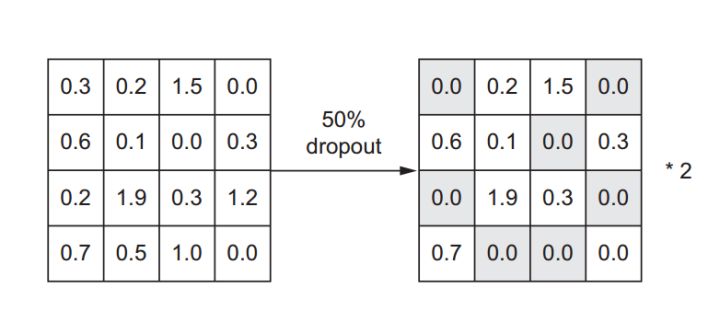
Dropout是最有效和最常用的神经网络正则化技术之一。Dropout在网络层训练期间随机失活(设置为零)该层的许多输出特征(节点)。 假设输入样本经过一个隐藏层后输出一个向量[0.2, 0.5, 1.3, 0.8, 1.1]。 在该层应用了Dropout之后,这个向量将出现几个为0的特征值:例如[0, 0.5, 1.3, 0, 1.1]。 Dropout的值表示节点被随机失活的概率,通常设置在0.2到0.5之间。在测试时间,则不再用dropout了,也就是说测试时所有的节点都要保留。这样就造成了测试与训练输出比例不匹配,测试时隐藏层活跃节点更多。因此,网络层的输出特征(节点)要乘上与Dropout率相等的因子来缩小,达到了类似L2正则化权重衰减的目的。因此Dropout在过程上与L1正则化相似,在最终结果上则与L2正则化相似。
假设一个网络层的输出layer_output的shape为(layer_size,features)。 在训练的时候,我们随机地将矩阵中的一小部分值置零:
# 在训练时,随机失活50%的节点
layer_output *= np.random.randint(0, high=2, size=layer_output.shape)
在测试时,我们乘以随机失活率缩小输出比例。在这里,我们缩小了0.5(因为我们之前随机失活了一半的节点单元):
# 测试时
layer_output * = 0.5
注意,这个过程可以在训练时通过两个操作实现,并且在测试时保持输出不变,这在实践中通常是这样实现的(见图4.8):
# 训练时
layer_output *= np.random.randint(0, high=2, size=layer_output.shape)
layer_output /= 0.5 # 注意,在这种情况下,我们扩大了输出,而不是缩小
这种技术可能看起来很奇怪和也很随意。为什么这会减少过拟合? Hinton说,他是受到银行所使用的防欺诈机制的启发。他说:“我去了我的银行。 出纳员不断变化,我问他们其中一个为什么要这样呢。 他说他不知道,他们就是这样来回换。我想这一定是因为欺诈机制需要员工之间的合作。 这使我意识到,在每个网络层中随机删除一个不同的神经元将防止“欺诈”,从而减少过度拟合。核心思想是,在一个图层的输出值中引入噪声可以打破特定模式 Hinton所称的欺诈),如果没有噪声存在,网络将开始记忆特定模式。
在Keras中,我们可以通过在激活层输出之后添加一个Dropout层实现Dropout:
model.add(layers.Dropout(0.5))
在IMDB例子中添加两个Dropout层,看看它们在减少过拟合方面的表现:
dpt_model = models.Sequential()
dpt_model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
dpt_model.add(layers.Dropout(0.5))
dpt_model.add(layers.Dense(16, activation='relu'))
dpt_model.add(layers.Dropout(0.5))
dpt_model.add(layers.Dense(1, activation='sigmoid'))
dpt_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
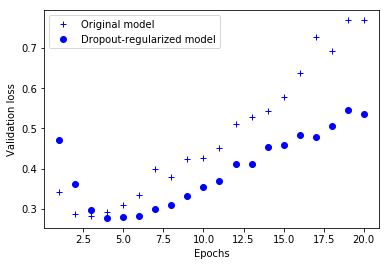
由图3.2显然可以得到:Dropout在4个epoch才出现过拟合,而原来的网络在三个epoch就出现过拟合。并且在出现过拟合后,验证集损失的增长速度明显比原来网络缓慢。
总结一下,神经网络中防止过拟合的常用方法:
- 获得更多的训练数据
- 缩小网络规模
- 权重正则化
- Dropout