共计 4002 个字符,预计需要花费 11 分钟才能阅读完成。
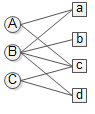
先举个例子
上面的二部图表示user A对item a和c感兴趣,B对a b c d都感兴趣,C对c和d感兴趣。本文假设每条边代表的感兴趣程度是一样的。
现在我们要为user A推荐item,实际上就是计算A对所有item的感兴趣程度。在personal rank算法中不区分user节点和item节点,这样一来问题就转化成:对节点A来说,节点A B C a b c d的重要度各是多少。重要度用PR来表示。
初始赋予 ,即对于A来说,他自身的重要度为满分,其他节点的重要度均为0。
然后开始在图上游走。每次都是从PR不为0的节点开始游走,往前走一步。继续游走的概率是停留在当前节点的概率是
第一次游走, 从A节点以各自50%的概率走到了a和c,这样a和c就分得了A的部分重要度。第一次游走结束后PR不为0的节点有A a c。
第二次游走,分别从节点A a c开始,往前走一步。这样节点a分得A 12∗α12∗α的重要度,节点c分得A 12∗α12∗α的重要度,节点A分得a 12∗α12∗α的重要度,节点A分得c 13∗α13∗α的重要度,节点B分得a 12∗α12∗α的重要度,节点B分得c 13∗α13∗α的重要度,节点C分得c 13∗α13∗α的重要度。最后PR(A)PR(A)要加上1−α1−α
经过以上推演,可以概括成公式:
\[ PR(j)= \begin{cases}
a*\sum_{i}\frac{PR(i)}{|out(i)|},\quad if(j \ne u) \\
(1-a)+a*\sum_{I}\frac{PR(i)}{|out(i)|},\quad if(j =u)
\end{cases}\]
u是待推荐的用户节点。
注意这里有一个现象,上述代码从节点b开始游走,最终算得的PR重要度最高的不是b,而是B。
personalrank经过多次的迭代游走,使得各节点的重要度趋于稳定,实际上我们根据状态转移矩阵,经过一次矩阵运算就可以直接得到系统的稳态。公式(1)的矩阵表示形式为:
\[r=(1−α)r0+αM^T(2)\]
其中r是个n维向量,每个元素代表一个节点的PR重要度,r0也是个n维向量,第i个位置上是1,其余元素均为0,我们就是要为第i个节点进行推荐。M是n阶转移矩阵:
\[ Mij= \begin{cases}
frac{1}{|out(i)|},\quad if(j \in out(i)) \\
0,\quad else
\end{cases}\]
按照矩阵乘法把(2)展开就可以得到(1)。
由(2)可以得到两种变形:
\[(I−αM^T)r=(1−α)r0\](4)
\[r=(I−αM^T)−1(1−α)r0\](5)
利用(4),解一次线性方程组就查以得到r,对r中的各元素降序排列取出前K个就得到了节点i的推荐列表。实践中系数矩阵\( ((I−αM^T) \)是一个高度稀疏的矩阵,解这种线性方程流行的方法是GMRES。另外在scipy中提供了多种稀疏矩阵的存储方法:coo,lil,dia,dok,csr,csc等,各有各的优缺点,dok可以快速的按下标访问元素,csr和csc适合做矩阵的加法、乘法运算,lil省内存且按下标访问元素也很快。更多内容参见scipy中的稀疏矩阵。
由于我们只关心r中各元素的相对大小,并不关心其真实值,所以(5)可以写为
\[r=(I−αM^T)^{−1}r0\](6)
矩阵\((I−αM^T)^{−1}\)乘以r0相当于是取出矩阵的第i列,因此为节点i进行推荐时对矩阵\((I−αM^T)^{−1}\)的第i列排序即可,所以求出矩阵\((I−αM^T)^{−1}\)的逆就得到了所有节点的推荐结果。
但是数据量很大的时候还是出现内存不足的现象,博主在自己的mac上测试10000*10000的矩阵需要消耗800m内存,网站的数据远远不止这些,那么额外消耗的内存会更多,接下来楼主贴出来的代码有点暴力计算的意思,但是会消耗不少的时间吧!
# -*- coding: utf-8 -*-
# @Time : 2018/4/16 上午10:55
# @Author : Tomcj
# @File : main.py
# @Software: PyCharm
# coding=utf-8
import numpy as np
import time
from scipy.sparse.linalg import gmres, lgmres
from scipy.sparse import csr_matrix
import os
from collections import defaultdict
class personalRank:
def __init__(self,path):
self.curr_dir = path
self.alpha = 0.8
self.zaful_data = []
self.node_degree = defaultdict(set)
self.data_for_csc = []
self.data_for_csc_row = []
self.data_for_csc_col = []
self.zaful_len=0
self.zaful_distinct_data=[]
self.users=set()
self.goods=set()
# 获取所有的数据
def getData(self):
# 实验测试使用zaful站采样的10000条数据
with open(os.path.join(self.curr_dir),'r') as fp:
fp.readline()
for line in fp:
data=line.strip().split("\t")
self.zaful_data.append([data[0],data[1]])
self.node_degree[data[0]].add(data[1])
self.node_degree[data[1]].add(data[0])
self.users.add(data[0])
self.goods.add(data[1])
#构造csr或则csc系数矩阵
self.zaful_distinct_data=self.node_degree.keys()
self.zaful_len=len(self.zaful_distinct_data)
zaful_data_map={ self.zaful_distinct_data[x]:x for x in xrange(self.zaful_len)}
for user,goods_id in self.zaful_data:
indexUser=zaful_data_map[user]
indexGoods=zaful_data_map[goods_id]
self.data_for_csc.append(-self.alpha*1.0/len(self.node_degree[user]))
self.data_for_csc.append(-self.alpha*1.0 / len(self.node_degree[goods_id]))
self.data_for_csc_row.append(indexUser)
self.data_for_csc_col.append(indexGoods)
self.data_for_csc_row.append(indexGoods)
self.data_for_csc_col.append(indexUser)
for x in xrange(self.zaful_len):
self.data_for_csc.append(1)
self.data_for_csc_row.append(x)
self.data_for_csc_col.append(x)
# 预测所有数据,基于item
def predictAll(self):
f=open('result.txt','w')
AA = csr_matrix((self.data_for_csc, (self.data_for_csc_row, self.data_for_csc_col)), shape=(self.zaful_len, self.zaful_len))
# 暴力穷举解法
try :
for xda in xrange(self.zaful_len):
if self.zaful_distinct_data[xda] in self.goods:
curr_goods=self.zaful_distinct_data[xda]
b = np.zeros((self.zaful_len, 1))
b[xda] = 1 * (1 - self.alpha)
r = gmres(AA, b, tol=1e-08, maxiter=1)[0]
# r = lgmres(AA, (1 - alpha) * r0, tol=1e-08,maxiter=1)[0] #lgmres用来克服gmres有时候不收敛的问题,会在更少的迭代次数内收敛
rank = {}
for j in xrange(self.zaful_len):
rank[self.zaful_distinct_data[j]] = r[j]
li = (sorted(rank.items(), cmp=lambda x, y: cmp(x[1], y[1]), reverse=True))
ele_cnt=0
for ele in li:
if ele[0] in self.goods and ele[0]!=curr_goods:
ele_cnt+=1
f.write(self.zaful_distinct_data[xda]+','+ele[0]+'\n')
finally:
f.close()
if __name__ == '__main__':
begin = time.time()
pr=personalRank('path')
pr.getData()
pr.predictAll()
end = time.time()
print end-begin


数据集请问可以传出来么?