共计 1677 个字符,预计需要花费 5 分钟才能阅读完成。
最近一些列的博客尽量使用口语化的方式来把问题说明白,一般情况下能把事情说的明明白白也可以变相的说明你对问题有一定的了解。
此处十一点四十多了码子有点困了。。。。continue
kmean聚类被使用的机会还是很多,计算比较简单,实现也简单。简单的方法也容易排查问题,kmean自身也有局限性,比如初始聚类中心点的选择对算法的影响以及聚类的个数k值的选择,面临大数据的时候算法计算的速度问题。
k值的选择如果有一定的先验知识的话可以确定大概的值,初始中心点的选择可以考虑使用kmean++算法或者canopy算法(此算法也存在参数的tuning的问题,但是也是一种思路),计算速度的问题也就是我们现在要聊的问题了。
这里所说的计算涉及到这一步,就是每一个观测点到聚类中心的距离计算,假设我们的聚类中心的个数比较多,每一次都要便利计算消耗的代价比较大,所以使用KD树数据结构来优化。
首先介绍一下KD树的构造过程
第一步:我们把n维特征的观测实例放到n维空间中,k-d tree每次通过某种算法选择一个特征(坐标轴),以它的某一个值作为分界做超平面,把当前所有观测点分为两部分,然后对每一个部分使用同样的方法,直到达到某个条件为止。
上面的表述中,有几个地方下面将会详细说明:(1)选择特征(坐标轴)的方法 (2)以该特征的哪一个为界 (3)达到什么条件算法结束。
(1)选择特征的方法
计算当前观测点集合中每个特征的方差,选择方差最大的一个特征,然后画一个垂直于这个特征的超平面将所有观测点分为两个集合。
(2)以该特征的哪一个值为界 即垂直选择坐标轴的超平面的具体位置。
第一种是以各个点的方差的中值(median)为界。这样会使建好的树非常地平衡,会均匀地分开一个集合。这样做的问题是,如果点的分布非常不好地偏斜的,选择中值会造成连续相同方向的分割,形成细长的超矩形(hyperrectangles)。
替代的方法是计算这些点该坐标轴的平均值,选择距离这个平均值最近的点作为超平面与这个坐标轴的交点。这样这个树不会完美地平衡,但区域会倾向于正方地被划分,连续的分割更有可能在不同方向上发生。
(3)达到什么条件算法结束
实际中,不用指导叶子结点只包含两个点时才结束算法。你可以设定一个预先设定的最小值,当这个最小值达到时结束算法
关于kd树的构造可以参考这篇文章kd树基本描述
ball tree
ball tree与kd树的不一样的地方主要是使用圆来代替矩形了。
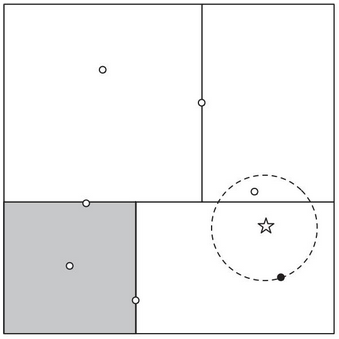
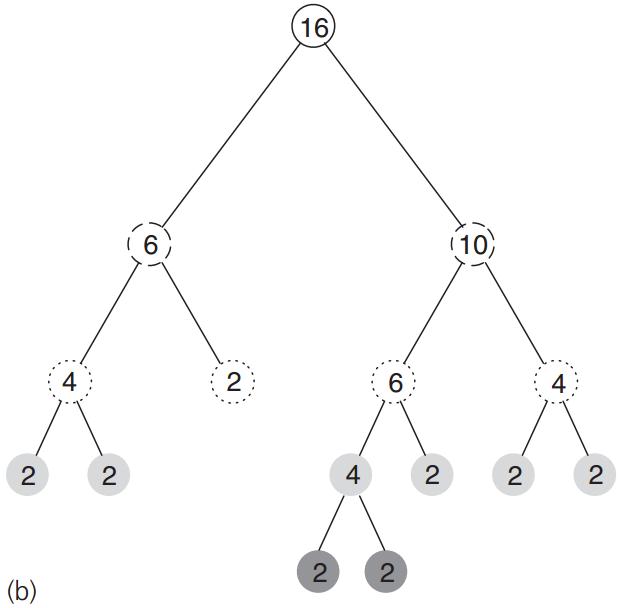
先看以下两个图
图a给出了圆形区域划分,图b示二叉树的基本描述,二叉树的每一个节点表示包含了多少个观察点,并且每一个节点会自带所有观测点的特征数据和数量,方便计算中心点。比如a图中最大的实线圆表示的就是根节点,这个节点包含了16个观测点,如果数据集就是上图描述出来的数据集,那么就可以说实线圆圈包含了所有的数据观测点。
kmeans使用ball tree
在k-means算法中使用k-d tree和ball tree效率更高,因为在此所有的观测点都是一起处理,而在k近邻中,测试的观测点单独处理。
首先,根据所有的观测点创建一个包含它们的k-d tree 或者是ball tree。
在k-means算法的每一次迭代中,设定的聚类中心集合为C={Ci,i= 1,…,k},每个簇中心有一个对应其归属它的观测点集合,初始为空。从根结点开始遍历树,直到找到叶子结点为止,判断其中的观测点距离哪一个中心近,然后赋给那个中心。有可能在浏览一个内部结点时,它所包含的点完全包含在一个聚类的区域内。这时只需要直接把其下所有的观测点加入到该聚类中即可。
我们可以在每个簇的中心点保存一个向量,保存聚类中点各个坐标之和和点的个数。在计算其中心点时只需一除即可。
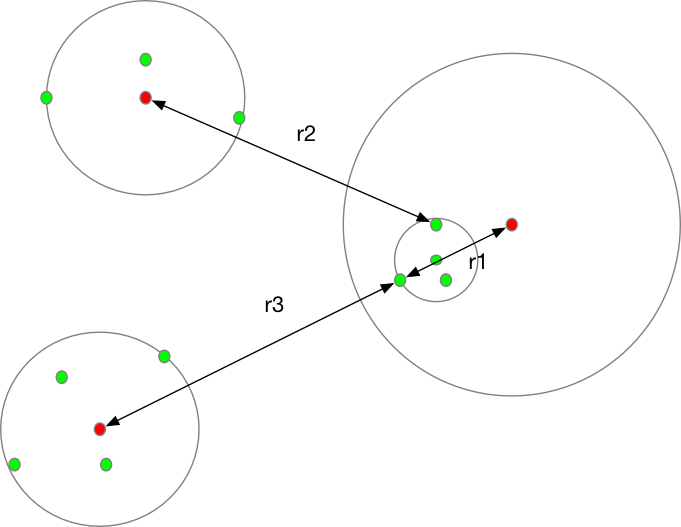
下面给出一个说明图,顺便安利一个软件omnigraffle,画图神器
上面三个大圆圈表示三个聚类簇,小圆圈表示一个balltree的超圆,此时超圆上的观测点与最右边的聚类簇中心的最远距离r1比r2,r3都要小,则将其归入最右边的聚类簇。r2,r3分别表示超圆观测点距离其他聚类簇中心的距离。