共计 717 个字符,预计需要花费 2 分钟才能阅读完成。
代价复杂度剪枝Cost-Complexity Pruning(CCP)
设初始\(k=0\),\(T=T_{0}\),\(\alpha\)为正无穷
自上而下的计算
\begin{align}
g(t)&=\frac{R(t)-R(T_{t})}{|N_{T_{t}}|-1}\\
\alpha&=min(\alpha,g(t))
\end{align}
g(t)&=\frac{R(t)-R(T_{t})}{|N_{T_{t}}|-1}\\
\alpha&=min(\alpha,g(t))
\end{align}
\(|N_{T_{t}}|\)表示子树包含的叶子节点个数
\(R(T)\)训练数据的预测误差(如基尼指数)=节点t上的数据占所有数据的比例*节点t的误差率
\(R(T_{t})\)是子树\(T_{t}\)的预测误差=子树\(T_{t}\)上所有叶子节点的预测误差之和;
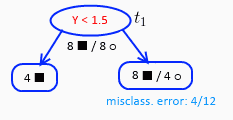
下面这棵树,有三个点 t1≡root,t2,t3
α(1)=0
计算每个点的 gt:
在此重点说明一下节点误差率的计算,比如t1节点下有8个黑方块和8和白圆圈,误差率的计算是认为较少的一部分样本数量作为误差样本(对每个叶子节点中的两个分类,个数少的是误差)
依此t2处黑色方块只有4个,那么误差率就是4/12
t2,t3 时的 gt 相等,此时我们可以选择剪枝少的点,那就是 t3 剪掉。
并且 α(2)=1/8
这时剩下 t1,t2,再继续计算 gt:
t2 的小,所以剪掉 t2:
并且令 α(3)=1/8
最后剩下 t1,计算后 gt=1/4,所以 α(4)=1/4。
如此我们得到:α(0)=0,α(1)=1/8,α(2)=1/8,α(3)=1/4
并且得到了相应的子树,
接下来就可以利用独立的验证数据集,计算每个子树的平方误差或者基尼指数,
选择误差最小的那个子树作为最优的剪枝后的树。
例子使用转载自https://www.jianshu.com/p/b90a9ce05b28
正文完
请博主喝杯咖啡吧!







第二次剪枝的时候,图表的α(t1)是不是算错了?