共计 1557 个字符,预计需要花费 4 分钟才能阅读完成。

前言
周五下午吧,翻开那本推荐系统的书,看到了MF和FM在一块,单从字面来看两个是完全对称的字母,但是却是不同的东西,今天把它们放在一起又是有关联的存在。
MF — Matrix Factorization — 矩阵分解
FM— Factorization Machine —因子分解机
从中文的翻译来看,都是有分解的字面在里面,其实这里面的确都会涉及到这些知识。
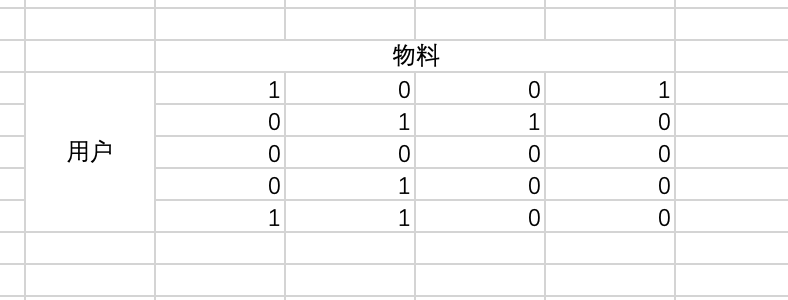
在学习MF的时候经常举例的就是那个movie数据集了,这里我简单的用excel表示了一下,图中就5个用户,4个物料,1表示用户喜欢这个物料,0表示不喜欢。MF的思想就是将上图这个矩阵拆分成两个小矩阵:
R=U*I
U表示用户,I表示物料,两者都存在同一个向量空间,那么可以直接基于embedding 查询的方式来找用户喜欢的物料。
但是考虑一些额外因素:1、一些用户给分偏高,一些用户给分较低,2、一些物品本就比较受欢迎,一些物品不被大众所喜爱,3、评分系统的固有属性,与用户物品都无关。因此,考虑到这些因素,将用户对物品的预测函数升级为:
R_{u,i}=bias_{init}+bias_u+bias_i+U*I
升级成这样也是为了后续对比MF的时候更加的方便对比说明。
因子分解机我就直接贴公示了,相比其原理就不在此赘述,
R_{u,i}=bias+\sum_{i=1}^{n}w_i*x_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}<v_i,v_j> *x_i *x_j
相同之处
现在说明FM和MF之间的关系,我们假设只用了用户id和物料id的one-hot编码,那么从之前的图来看,特征向量的长度是9,用户5物料4,我们看下第4行即第四个用户,那么现在的向量就是[0,0,0,1,0,0,1,0,0]
将这个向量带入到FM的计算公式可以得到
R=bias+w_4+w_7+<v4,v7>
因为只有4和7位置才有对应的数据,所以这个结果的形式对比MF的结果基本上都是一模一样。那么在回头看,我们只用了id类特征,殊不知其实用户和物料本身还有很多其他的特征,比如电影的时长,导演等等。
所以到这里得到的结论就是MF是FM的精简版本。
不同之处
- 「输入数据的形式不同。」 一般来说,FM的输入数据是一个实值特征向量(如图1的每一行),相当于是对多个one-hot特征的拼接;MF的输入数据是一个二元组(u,i),u为用户ID,i为物品ID。往往对于FM和MF理解的难点在于此,一个数据形式为one-hot,一个数据形式为标量ID。只不过MF中的数据只有user和item,因此可以通过标量ID直接查询对应的隐向量,而FM则需要通过one-hot的形式与隐向量矩阵做乘得到对应的隐向量。
- 「参数矩阵的不同。」 往往我们在FM模型中只初始化一个参数矩阵V(k*f),其中f为特征的数目;MF模型由于只涉及user和item的隐特征,因此可以分别学得一个用户矩阵U(m*d)和物品矩阵I(n*d)。如果FM中只有user和item的特征时,k=m+n。因此,只不过MF为了方便,把user和item分开进行初始化,其实类似于FM只初始化一个矩阵未尝不可,只不过需要注意user和item的小标不要重复,比如user从1开始,那么item很可能需要从m+1开始。
- 「融合附加信息的方式不同。」 他们输入数据的形式决定了他们融合附加信息的形式不同。直观来讲,FM融合附加信息的方式更直接。比如FM融合边信息直接在列的维度拼接特征即可,比如增加性别、年龄等信息;而MF融合边信息不能直接在输入数据上拼接,而是需要通过增加正则项约束,或者在预测函数上做文章。更具体的融合方式可参考之前的博文推荐系统之矩阵分解家族,可见MF也可以方便快捷的融合各种附加信息。


