共计 672 个字符,预计需要花费 2 分钟才能阅读完成。
提前说一句不太好听的话,其实这个论文这个环节我看的懵逼,不是太懂。公式推理看起来都是对的,从上往下推是可以推的通,但是给我的感觉是说了跟没说一样,还是不太理解正在解决PIP的思路。
所以这篇文章算不上论文解读,应该只是自己的疑问通过文字描述一遍,看看有咩有新的想法。。。。
第一个疑问点,为什么将样本分为k个,这个跟放在一起有什么区别?

说是在第K个盒子里,在点击事件上观测的分布是独立于反事实cvr预估,这个是嘛意思?实在是不理解。
但是看18公式又是比较简单,就是针对click=1和click=0的样本的loss估计。正常每个盒子里的样本不都是满足这个公式,即使不进行样本划分不都是一样?所以这个样本划分的含义是啥?
然后在看下面的推理哈
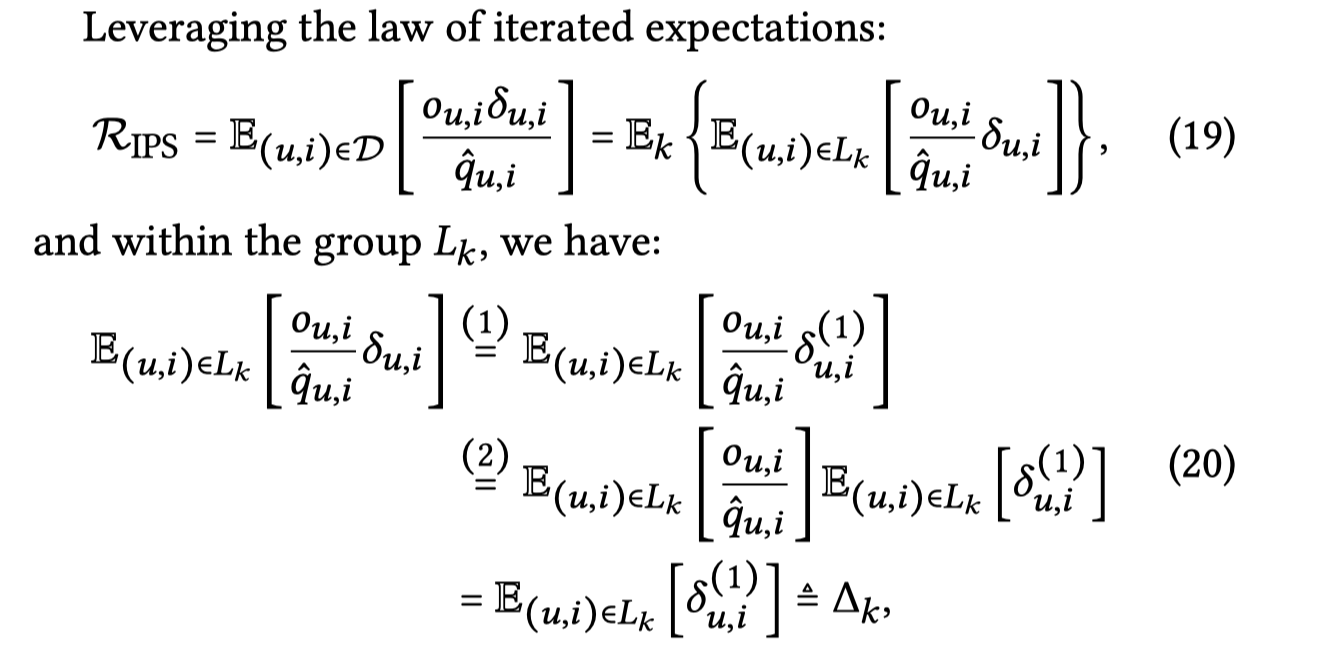
19公式其实就是将全空间到K个子空间的转化。
公式20中最后一步转化其实有点疑问,E_(u,i)[\frac{o_{u,i}}{\hat q_{u,i}}]这个被消除了,对于点击样本o_{u,i}=1但是分母应该还是预估值,难道是对所有的点击样本期望是1?这个是ips里调权的参数,就是之前文章里介绍的ctr tower输出的pctr的倒数,这么看也不太是这么回事?
接着就直接得到结论了。。。
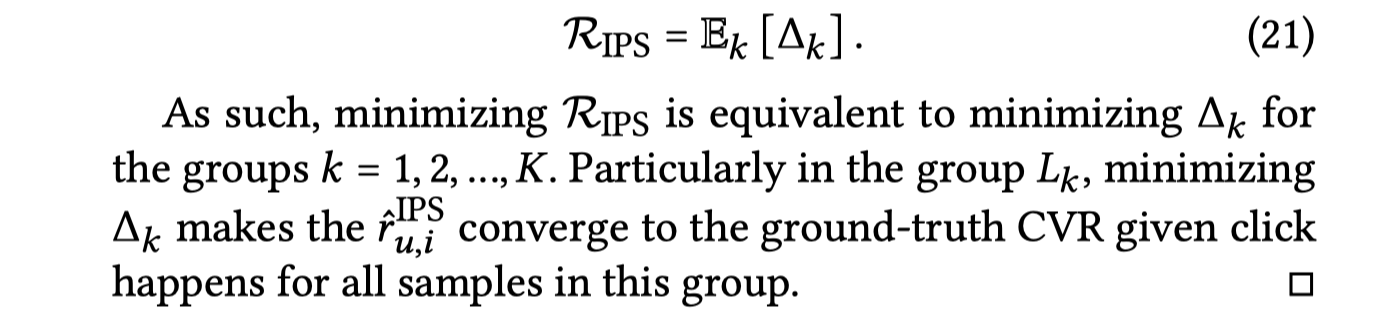
反正我还是没看懂啊!
其实说实话到这里IPS的论证是完了,但是究竟IPS真的是做无偏估计?看过之前一个大佬的解释,使用ctr高低来决定样本权重是否真的合理?
- ctr高并且转化了,无可厚非,样本权重低一点正常?
- ctr高但是未转化,这个不符合常理,是不是权重应该更高?
- 全用pctr倒数当权重,是不是不太合适?


