共计 2609 个字符,预计需要花费 7 分钟才能阅读完成。
假设您有一个数组,其中第i个元素是第i天给定股票的价格。
设计算法以找到最大利润。 您最多可以完成两笔交易。
注意:您不得同时进行多笔交易(即,您必须在再次购买之前卖出股票)。
例1:
输入:[3,3,5,0,0,3,1,4]
产量:6
说明:在第4天买入(价格= 0)并在第6天卖出(价格= 3),利润= 3-0 = 3。
然后在第7天买入(价格= 1)并在第8天卖出(价格= 4),利润= 4-1 = 3。
例2:
输入:[1,2,3,4,5]
产量:4
说明:在第1天买入(价格= 1)并在第5天卖出(价格= 5),利润= 5-1 = 4。
请注意,您不能在第1天购买,在第2天购买并在以后出售,就像您一样
同时参与多个交易。 您必须在再次购买之前出售。
例3:
输入:[7,6,4,3,1]
输出:0
说明:在这种情况下,没有进行任何交易,即最大利润= 0。
解法
因为之前做过一导easy的题,它是只允许你成交一次,然后获取最大的利润,这道题最大交易次数只允许交易两次,那么我一开始的想法是这个样子:
- 先算出只交易一次的最大利润max_profit_once
- 遍历每一天,计算当前第i天之前与第i+1天以后两者最大利润之和即left_profit+right_profit
- 然后比较第二步与第三步利润大小,返回最大值即可
这个测试的代码提交以后在200个case中第199个case失败了,原因在于超时了
第199个case是一个很长的测试样例,因此使用之前的方法穷举获取很耗时。
dp动态规划
这道题是一个动态规划题,既然涉及到动态规则规划那就要知道我们现在求解的大问题是啥,如何拆分成小问题?
- 大问题就是N天内限定最大两次交易的情况下我们能够获取的最大利润
- 小问题:
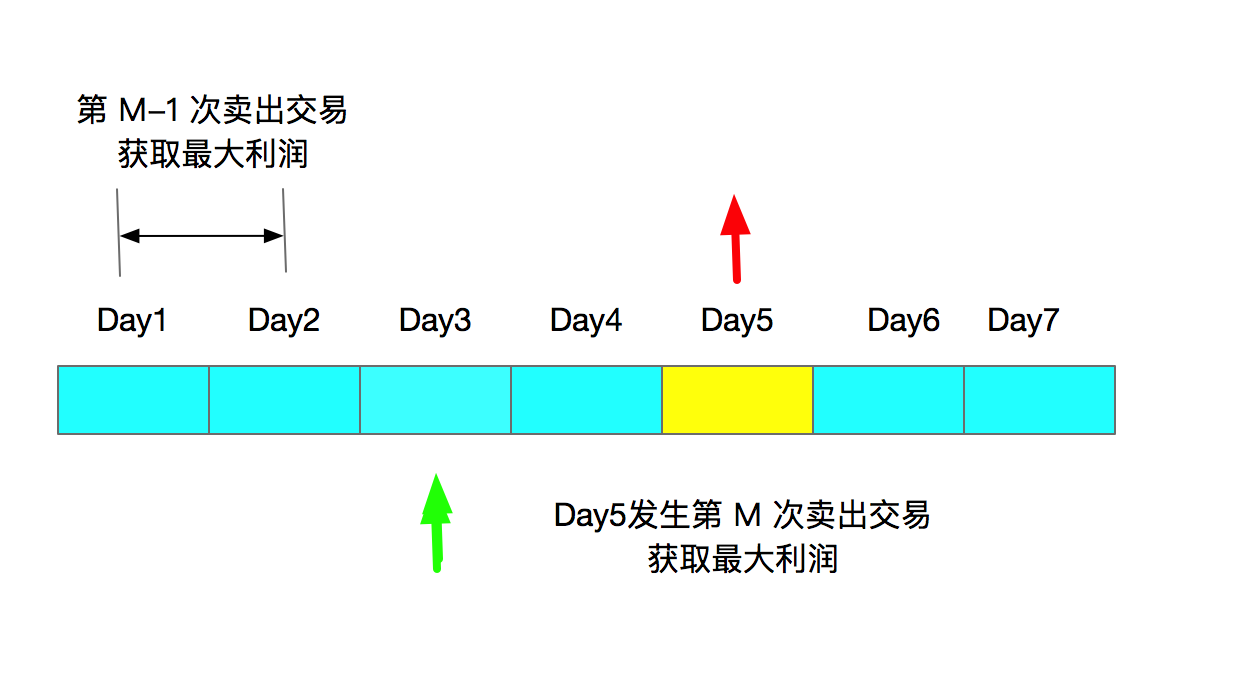
从上面图可以看出当我们在Day5 发生交易的时候,此时是处于第M次卖出交易,那么之前肯定在某一天发生买入交易,图中给出了Day3发生买入交易,那么第M次交易产生的最大收益可以获知。那么剩下的就是要去求解第M-1次交易获取的最大收益,按照图示的例子就是要去计算Day1和Day2产生的收益,如果时间的跨度更长,那么我们会一直计算到第一次交易获取的利润
累加M次交易获取的利润之和(存在多种情况下M次交易之和),取出最大值就得到我们想要的答案了
所以我们可以得到下面的公式:
Profit(T,M)=Profit(T-n,M-1)+Profit(T-n-m,M-2)+…..
解法
代码说明
第一个 if 判断就是当prices列表长度小于2的时候直接返回0,因为你们有任何机会去出手交易。
m就是我们定义的交易最大次数,该题是2次
DP是我们定义的保存第m次以及第N天交易获取的最大利润矩阵,为什么会定义[m+1,N]维,这在后面迭代计算的时候
会用到,初始化就是矩阵里面所有的元素都为0
第一个 for 循环是循环迭代交易次数,即仅在 i 次交易内得到的最大利润
第二个for 循环是迭代所有的天数,因为可以在任意一天发生交易
if i == 0 or j == 0该子嵌套条件说明,当交易次数为0的时候或者第一天开盘,你只能买入没法卖出,所以满足此条件下的利润值都是为0
的,因为你都不满足交易的条件
所以只有在当交易次数i为1且j>0的时候开始才开始有机会交易,那么就到了嵌套 else 处理部分了
DP[i][j] = DP[i][j - 1]DP[i][j] 直接使用 DP[i][j – 1] 赋值,只是相当于初始化,当前第 j 天你不卖出交易,那么你的利润就是昨天的利润。
接下来循环遍历 k , k的取值返回是 0 到 j-1
意思就是在0到j-1天内,用户必须在这其中一个买入,然后在第 j 天卖出
prev变量是获取第 i-1 次第 k-1天 获取的最大利润,因为当前是第 i 次交易,我们要的是总的最大利润,所以我们要把之前的利润都要加起来。
DP[i][j] = max(DP[i][j], prev + prices[j] - prices[k])这一步:还记得在算DP[i][j] 之前我们使用 j-1 天的数据初始化了一下
prev + prices[j] – prices[k] 就是第 j 天获取的最大利润了,但是我们也要跟前一天的数据比较,因为这天交易可能是亏的,如果亏损了,那么证明今天不适合交易,那么还是保留之前的交易记录,当然 j 天的利润还是沿用之前的利润数据,同时第 j 天就不应该发生卖出交易。
k 值循环就是在寻找局部最优解,就相当于DP问题小问题求解优化。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices)<2:
return 0
m = 2
n = len(prices)
DP = [ [0]*n for x in range(m+1)]
for i in range(m+1):
for j in range(n):
if i == 0 or j == 0:
DP[i][j] = 0
else:
DP[i][j] = DP[i][j - 1] for k in range(j):
prev = 0 if k == 0 else DP[i - 1][k - 1]
DP[i][j] = max(DP[i][j], prev + prices[j] - prices[k])
return DP[m][n - 1]
优化
看完上面是不是觉得这个问题已经可以解决了,此时如果你提交上面的代码仍然是Fail,依然会提示你超时,也是发生在第199个case,因为你在时间复杂度是O(kn^2)
下面代码与之前的不同点就是在于 k 循环的优化
其实按照现在的代码逻辑我们每一步都是局部最优,那么我们在计算DP[i][j] 就只使用
DP[i][j-2]-prices[j-1]+prices[j]与DP[i][j-1]即可,至此完成了这道题的求解
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices)<2:
return 0
m = 2
n = len(prices)
DP = [ [0]*n for x in range(m+1)]
for i in range(m+1):
tempMax=-sys.maxsize-1
for j in range(n):
if i == 0 or j == 0:
DP[i][j] = 0
else:
prev = 0
if j >= 2:
prev = DP[i - 1][j - 2]
tempMax =max(tempMax, prev - prices[j - 1])
DP[i][j] = max(DP[i][j - 1], tempMax + prices[j])
return DP[m][n - 1]